| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 뉴럴네트워크
- Spiking Neural Network
- Generative Model
- Bagging
- 이상 탐지
- ae
- MNIST
- rnn
- 머신러닝 논문리뷰
- 딥러닝
- 논문 리뷰
- 레이텍
- 머신러닝
- 논문 해석
- 인공신경망
- autoencoder
- MLE
- Machine Learning
- 이상 현상 탐지
- Deep Neural Network
- Python
- Snn
- ML
- 논문리뷰
- map
- anomalydetection
- Fast Fourer Transform
- Wavelet Transform
- 기계학습
- Deep Learning
- Today
- Total
MATH & ML
머신러닝의 전반적인 흐름(에러 관점, 확률론적인 관점 그리고 MLE와 MAP차이 및 연관성) 본문
네이버 d2에서 이활석님께서 아주아주 최근에 발표하신 영상과 슬라이드를 공유해 놓으셨다.(링크는 맨아래)
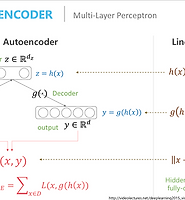
목적은 autoencoder를 설명하기 위함인데 이를 위해 초반부분에 deep Neural Network와 관련된 기초적인 내용을 먼저 설명해주셨는데
영상을 보면 볼수록 설명을 쉽게 정리잘되게 해주셔서!
머신러닝의 전반적인 내용을 이곳저곳 찾아보고 영상도 보며 큰 그림을 정리해보려 한다.
먼저 머신러닝에서 하는 건 큰 그림으로 볼때 다음 사진처럼 정리 할 수 있다.
데이터가 주어지면 그걸로 어떤 알고리즘, 즉 모델을 학습하고, 이제 그 학습된 모델을 실제 정답의 모델과 거의 미슷하다고 가정하고 거기에 test data를 넣어서 나온 결과가 우리가 원하는 결과이다. (보니까 이건 supervised learning인 것 같다)
(출처 : http://sanghyukchun.github.io/57/)
그러면 이 가운데에 있는 알고리즘 학습, 즉 모델 학습이라는 건 과연 어떤것일까.
이 학습되는 알고리즘이라는건 한마디로 x를 적절한 y와 연결시켜주는 함수라고 볼 수 있다.
이 학습 방법을 크게 두 가지로 볼 수 있는데, 첫째 함수를 가정한 후에 그 에러를 최소화! 둘째 y에 대한 확률을 최대화하는 관점이다.
이렇게 2가지 관점에서 보자면, 첫째를 위한 방법 중 하나가 그 함수를 어떤 식으로 가정을 한 후에(예를들어 f(x)=ax+b) 그 함수에 대입한 결과와 실제 아웃풋과의 에러를 최소화 하는 방향으로 계속해서 a와 b를 업데이트 시켜 가장 최적화된 a, b를 찾는, 즉 함수를 찾는 것이다. 이러한 관점에서 방법들 중 하나가 neural network를 이용해서 backpropagation방법을 사용하는것이다. 다른 2번째 관점은 확률론 적인 관점이며, 그때 사용하는 방법으로 MLE, MAP를 쓰는 것이다.
1. 1번째 관점
1번째 관점에서, NN에서 Loss function을 무엇으로 정하는지에 따라 결과가 다른데, backpropagation 방법을 이용하여 weight를 업데이트 시키위해서는 다음 두 가지 조건이 만족되는 Loss function을 골라야 하는데 아래의 두 가지를 만족시키는 가장 대표적인 두 가지 에러 함수가 MSE(Mean Square Error)와 CE(Cross Entropy)이다.
조건1-NN의 전체 Loss는 각각의 training sample들의 Loss의 총합이다.(곱같은것으로 하지않고 합으로 한다! 아마도 미분을 위해서인듯)
조건2-각 training sample의 Loss는 NN의 최종 출력값에 관한 함수이다.(가운데 히든레이어에서의 값으로 Loss를 정의할 수 도 있는데 그렇게 안하고 마지막 최종 출력값에 관한 함수!로 한다는 뜻이다)
그러면 언제 MSE를 쓰고 언제 CE를 쓰느냐? 발표에 따르면 MSE와는 달리 CE는 출력 레이어에서의 에러값에 activation function의 미분값이 곱해지지 않아 gradient vanishing problem에서 좀 더 자유롭다. (이 말의 의미는 계속 작은 값이 곱해지다보면 러닝 레이트가 너무 작아져서 weight 업데이트가 너무 조금씩 되어 학습이 느려지는데 CE는 이에 대해 좀 더 자유로워서 학습이 좀 더 빨리 된다) 그러나 레이어가 여러 개가 사용될 경우에는 결국 activation function의 미분값이 계속해서 곱해지므로 gradient vanishing problem에서 완전 자유로울 수 없다.
그래서 최근 유행해온것이 ReLU라는 activation 함수를 이용해서 미분값이 1보다 작지않게해서 무조건 1 혹은 0이므로 이러한 관점에서는 아주 좋은 해결 방안이다.
2. 2번째 관점
이를 backpropagation의 관점이 아닌 위에서 말했던 2번째 관점, 즉 확률론적인 관점으로 볼 수도 있는데, x에 따라 y가 어떤 확률 분포를 따른다고 가정한 후, x가 주어졌을 때 그때에 따라 y가 될 확률을 최대화 시키는 그 확률 분포를 구하는 것이다. 이 때 확률 분포를 구한다는 말은 확률 분포를 결정하는 어떤 변수들을 설정하여 그 변수들을 결정하는 방식이다. 예를 들면 Normal distribution이라면 그 분포의 평균과 표준편차를 변수로 설정하여 그 두 변수를 찾을 수도 있고 하나만 설정하여 하나만을 찾는 방식으로 할 수도 있다.
사실 x에 따른 y의 확률분포를 가정한다는 말은 y를 x에 대한 함수 식으로 가정을 한 후에, 그 함수의 마지막에 에러 텀을 추가하여 그 에러 텀에 대한 확률분포 가정을 하는 방식하고 똑같다고 볼 수 있다.
이와 관련하여 아주 신기한 사실 중 하나는 이 y가 따른 분포를 어떻게 가장하느냐에 따라서 1번째 관점에서 논의한 에러함수와 연관이 있는데,
노말분포 가정 & MLE이용 -> MSE를 최소화 시키는것과 동치
베르누이분포 가정 & MLE이용-> CE를 최소화 시키는것과 동치
가 된다.
즉 이 관점에서 볼때, y가 연속적인 분포라 하면 MSE를, y가 discrete 분포라 하면 CE를 쓰는것이 더 적합하다고 생각 할 수 있다.
그렇다면 매번 나오던 얘기인 MLE와 MAP는 과연 어떻게 쓰이는 것인가! y가 따른다고 가정한 확률 분포를 최대화 시키는 과정에서 쓰였다. 그 y_1 ~ y_n 이 어떤 분포를 따른다고 가정했을 때, 어떤 평균 혹은 표준편차를 선택할 것인가! 를 MLE 는 likelihood 함수를 최대화 하는 것으로, MAP는 posterior 함수를 최대화 하는 것으로 보는 것이다. 이 때 헷갈리지 않으려면 이렇게 기억하면 될 것 같다. 그 변수에 대한 사전에 지식, 즉 prior distribution을 아는 경우에 기존 MLE에 그 prior텀을 더하여(log likelihood로 생각하면 더한다고 볼 수 있다) 생각함으로서 더 최선의 변수를 선택 할 수 있게 하는 것이 MAP라고 보면 좋을 것 같다. 또한 MLE는 likelihood 함수인 f(x|theta) 에서 어떤 theta가 주어졌을 때 데이터의 확률이 최대화 되는지 그 theta라는 파라미터를 구한다고 생각한다면, MAP는 posterior 함수인 f(theta|x) 에서 데이터들이 다 주어져 있을 때 어떤 theta일 확률이 가장 큰지를 구하는 것이다. 사후확률이라는 말은 주어진 데이터에 대해 파라미터가 될 확률을 나중에 선택하기 때문에 붙여진 이름인 것 같다.
이러한 MLE와 MAP의 차이는 1차 linear Regression에서 쉽게 이해할 수 있다, 이에 관련해서는 수업 발표를 위해 만든 밑에 슬라이드 사진들을 참고하자~
신기하게도 W에 대한 선 지식이 있어서 노말이라고 가정하고 계산한 결과는 기존 우리가 알던 리그레션에 regular 텀을 더해준 리지 리그레션이 되는 것을 볼 수 있다.
참고로 나중에 포스팅할 Autoencoder 그리고 Variation Autodencoder는 각각 P(X|X), P(X)를 최대화 시키는 2번째 관점으로서 접근을 시작한다.
'Machine Learning' 카테고리의 다른 글
| Autoencoder란 개략적 설명과 종류 (0) | 2018.06.15 |
|---|---|
| dimension reduction에 관련된 몇 가지 관점 (0) | 2018.06.07 |
| capsnet(캡스넷) (0) | 2018.04.25 |
| sequence to sequence(seq2seq) (0) | 2018.04.23 |
| RNN(Recurrent Neural Network) (1) | 2018.04.23 |